Ergänzung 1.7: Strahlungsgrößen und Radiometrie (4/9)

Die Strahlstärke ... weiter von der vorherigen Seite

Für einen isotropen Strahler mit richtungsunabhängiger Strahlstärke kann das Integral gelöst werden. Bei einem kegelförmigen Raumwinkel wie in der Grafik in der linken Spalte der vorherigen Seite, der aber in Richtung Zenit orientiert ist, variiert der Azimutwinkel $φ$ von 0 bis $2 π$ . Der Zenitwinkel $ϑ$ variiert von 0 bis zum halben Öffnungswinkel $ϑ'$ :

Φ = I \int_{ϑ = 0}^{ϑ'} \int_{φ = 0}^{2 π} sin ϑ d ϑ d φ = I \cdot 2 π (1 - cos ϑ')

Diese Lösung ist eine Alternative zu der Rechnung im Beispiel Effizienz eines Linsenkollimators auf der vorherigen Seite.

Aufgabe 2: Isotrope Strahler ↓

Bei anisotropen Strahlern, deren Emission symmetrisch um eine Achse ist, kann das Integral teilweise gelöst werden. Hierfür betrachten wir die folgende Grafik, in der ein axialsymmetrischer Raumwinkel um die Vertikalachse (die Zenitachse) dargestellt ist und wie ein um die Halbkugel gelegtes Band erscheint. Dieser ebenfalls differenzielle Raumwinkel ist:

d Ω = \frac{d a}{R^{2}} = \int_{φ = 0}^{2 π} sin ϑ d ϑ d φ = 2 π sin ϑ d ϑ

Mit der Annahme einer nur vom Zenitwinkel ϑ abhängigen Strahlstärke $I (ϑ)$ kann die Emission über den Azimutwinkel φ integriert werden:

Φ = \int_{ϑ_{1}}^{ϑ_{2}} \int_{φ = 0}^{2 π} I (ϑ) sin ϑ d ϑ d φ = 2 π \int_{ϑ_{1}}^{ϑ_{2}} I (ϑ) sin ϑ d ϑ

Gleichungen ↓

Integration über den Azimutwinkel φ von 0 bis

2 π

ergibt ein Band um die Kugel unter dem Zenitwinkel ϑ mit der Breite Rdϑ. Wegen der differenziellen Breite ist auch dieses Band ein differenzielles Flächenelement da.

Aufgabe 3: Anisotrope Strahler ↓

Die axialsymmetrische Strahlstärke einer Lampe sei durch

I (ϑ) = \frac{1}{2} I (ϑ = 0) (1 + cos ϑ)

gegeben.

Skizzieren Sie bitte die Verteilung der Strahlstärke über den Zenitwinkel ϑ von 0 bis 180°.
Berechnen Sie die insgesamt emittierte Strahlungsleistung als Funktion der Strahlstärke für ϑ = 0.

Prüfen Sie Ihre Ergebnisse auf dieser Seite!

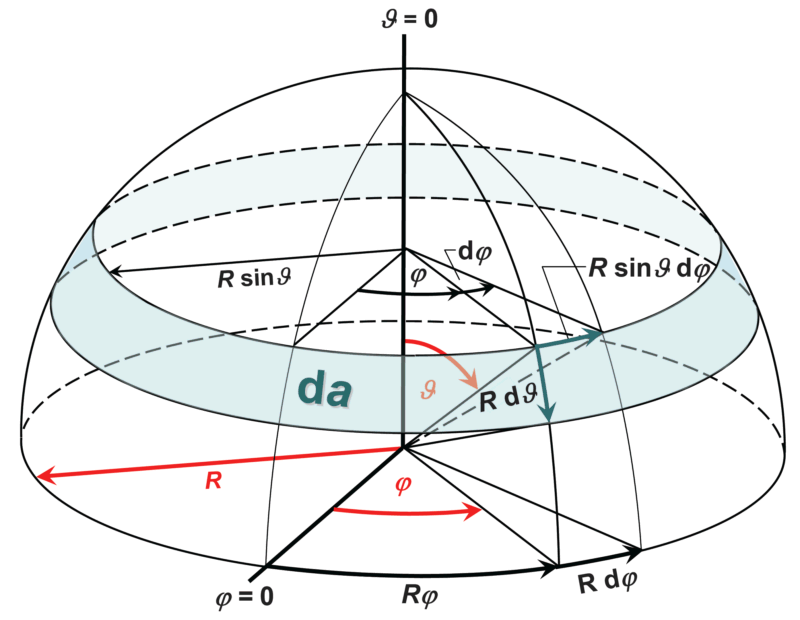
Eine besondere Form anisotroper Strahler sind die Kosinus-Strahler oder Lambert-Strahler, benannt nach dem Mathematiker und Physiker Johann Heinrich Lambert (1728-1777). Diese Strahler werden in der Ergänzung 1.8 erörtert.

Methoden zur Messung der Strahlstärke werden im Abschnitt über die Strahldichte vorgestellt.

Spektren der Erde

Ergänzung 1.7: Strahlungsgrößen und Radiometrie (4/9)

Die Strahlstärke ... weiter von der vorherigen Seite