Flugzeuggestützte Meeresüberwachung 3:
Interferenz von Öl auf dem Wasser

Szenario

Misst man die Mikrowellenausstrahlung (Frequenzbereich 1 ... 100 GHz) von Meerwasser über großen Ölflecken, dann findet man bei bestimmten Werten der Ölschichtdicke Maxima und Minima in der Signalhöhe (siehe Graphik unten). Dies entsteht durch konstruktive und destruktive Interferenz innerhalb der Ölschicht, die für Mikrowellen durchsichtig ist. Der Effekt hängt daher von der Frequenz (oder: Wellenlänge) ab. Er kann genutzt werden, um Ölschichten an der Meeresoberfläche mit einem abbildenden Mikro- wellenradiometer zu kartieren (Bilder rechts).

Strahlungstemperatur von Öl in absoluten Temperaturen (Kelvin-Skala) in Abhängigkeit von der Dicke eines Ölfilms in Millimeter bei drei Frequenzen im Mikrowellenbereich. Der Beobachtungs- winkel des Radiometers an der Oberfläche des Öls (zum Lot hin bestimmt) ist 41° (5 GHz), 54° (17 GHz) und 50° (34 GHz).

Links: Geometrie des scannenden Mikrowellenradiometers. Rechts: Ölfleck aus 17 m³ schwerem Schiffstreibstoff, mit einem MWR-Scanner bei 32 GHz kartiert. Der Beobachtungs- winkel des Radiometers an der Wasseroberfläche (zum Lot hin gemessen) ist 40°. Die höchste Änderung der Strahlungstemperatur ist 17 K.

Im Spektralbereich der Mikrowellen haben Öl und Wasser folgende Eigenschaften:

Öl ist durchsichtig und somit nicht absorbierend. Wegen des Kirchhoffschen Gesetzes emittiert es daher keine Temperaturstrahlung. Im Mikrowellenbereich ist die relative Dielektrizitätszahl von Mineralölen ε_r=2,0, und es folgt für die Brechzahl: n=1,41 (siehe Ergänzung 3 der SEOS-Lerneinheit Spektren der Erde).
Meerwasser ist wegen der hohen elektrolytischen Leitfähigkeit durch die gelösten Salzionen für Mikrowellen hoch absorbierend und somit nicht durchsichtig. Die relative Dielektrizitätszahl von Meerwasser ist ε_r=90, and es folgt für die Brechzahl: n=9,4 (im Sichtbaren ist n=1,33). Die Wasseroberfläche emittiert wegen des hohen Absorptionsvermögens Temperaturstrahlung, wieder in Übereinstimmung mit dem Kirchhoffschen Gesetz. Die spektrale Verteilung der Temperaturstrahlung folgt aus dem Planckschen Strahlungsgesetz, mit einem Maximum im Infrarot bei Wellenlängen um 10 μm. Hier berücksichtigen wir jedoch nur den Spektralbereich der Mikrowellen. Die Strahlung kommt aus der obersten Schicht des Meerwassers bis zu einer Tiefe, die etwa der Wellenlänge entspricht, also ca. einige Zentimeter.

Um das Auftreten von Interferenzstreifen besser zu verstehen, betrachten wir die Ausstrahlung von Mikrowellen durch Meerwasser, sowie eine Ölschicht auf der Wasseroberfläche. Die Welle breitet sich durch das Öl aus und wird teilweise an der Öl-Luft - und der Öl-Wasser - Grenzfläche reflektiert. Wir untersuchen solche Wellen, die nach einigen Reflexionen schließlich in die Luft hinein gebrochen werden und sich in Richtung Detektor des Mikrowellenradiometers ausbreiten.

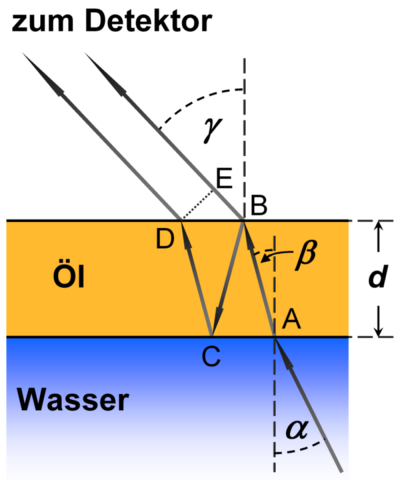
Nun betrachten wir einen Strahlengang mit dem Einfallswinkel α und Brechwinkel β an der Grenzfläche Öl-Wasser. Es wird angenommen, die Ölschicht hat eine konstante Dicke d. Die Wellen werden an der Öl-Luft - Grenzfläche teilweise reflektiert und transmittiert; die entsprechenden Einfalls- und Brechwinkel sind β und γ. Das Gesichtsfeld des Mikrowellenradiometers hat einen Einfallswinkel an der Wasseroberfläche, der dem Winkel γ entspricht.

Nach dem Snelliusschen Reflexionsgesetz ist in Punkt B der Einfallswinkel gleich β, und dies trifft auch für den Reflexionswinkel in Punkt B zu. Dieser Wert gilt auch in Punkt C, sowie für den Einfallswinkel in Punkt D, da die beiden Grenzflächen Öl-Wasser und Öl-Luft parallel sind.

Für die Brechwinkel der Wellen an beiden Grenzflächen ergibt sich aus dem Snelliusschen Brechungsgesetz:

\frac{sin α}{sin β} = \frac{n_{Ö l}}{n_{W a s s e r}} \frac{sin γ}{sin β} = \frac{n_{Ö l}}{n_{L u f t}} (mit n_{L u f t} = 1)

Eine Ölschicht mit Dicke d an der Wasseroberfläche, und Mikrowellen mit einem Strahlengang, der zum Detektor des Radiometers führt. Teilweise Reflexion an den Wasser-Öl-Luft - Grenzflächen führt zu Interferenzstreifen, wie man sie in der Grafik auf der Seite oben sieht.

Fragen

Bitte zeichnen Sie zwei Wellen, die an den Punkten B und C starten und eine Phase haben, welche zu konstruktiver und destruktiver Interferenz führen, und somit zu Maxima beziehungsweise Minima des Empfangssignals.
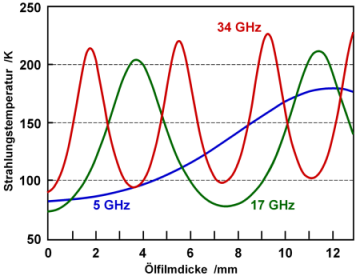
Berechnen Sie die Wellenlängen der Mikrowellen in Luft und Öl, die den Frequenzen 5, 17 and 34 GHz entsprechen. Stehen die Wellenlängen in Übereinstimmung mit den Schichtdicken von Ölfilmen, bei denen Maxima und Minima in der Strahlungstemperatur beobachtet werden, wie in der Abbildung oben gezeigt?
Würden Sie mit den oben genannten Brechzahlen für Wasser und Öl den in der Grafik rechts eingetragenen Einfallswinkel α und Brechwinkel β als richtig gezeichnet beurteilen? Prüfen Sie dies mit Hilfe des Snelliusschen Brechungsgesetzes! Beginnen Sie hierfür mit γ=50°, was dem typischen Beobachtungswinkel von Mikrowellenradiometern entspricht (siehe die Bildunterschrift in der Grafik oben), und berechnen Sie die Winkel β und α. Variieren Sie ggf. den Winkel γ.
Können Sie den MWR-Scanner empfehlen, um
a) dünne Ölfilme infolge geringer Öleinleitungen von großen Ölmengen zu unterscheiden, wie sie durch Schiffsunfälle verursacht werden?
b) eine Überwachung vorsätzlicher Einleitungen kleiner Ölmengen von etwa 100 Liter pro Seemeile durchzuführen?
c) Ölbekämpfungsschiffe nach unfallbedingten Einleitungen großer Ölmengen bei den Reinigungsoperationen zu unterstützen?
In das Meer eingeleitetes Öl altert infolge Wind und Wellen. Insbesondere mischen sich kleine Wassertropfen in das Öl, was zu einer Emulsion (‘Chocolat Mousse’) führt. Ist es möglich, mit dem MWR-Scanner gealtertes Öl an der Wasseroberfläche zu detektieren und die Schichtstärke zu bestimmen?
Ein weiterer Alterungseffekt ist die Verdunstung leicht flüchtiger Komponenten, was zu einer Zunahme der Dichte des Öls führt. Die Dichte kann schließlich diejenige des Wassers übersteigen. Dann taucht das Öl ab und treibt in der Wassersäule. Wäre es möglich, abgetauchtes Öl mit einem MWR-Scanner zu finden?

Lösungen

In Luft: 5 GHz - 6,0 cm; 17 GHz - 1,76 cm; 34 GHz - 0,88 cm.
In Öl: 5 GHz - 4,26 cm; 17 GHz - 1,25 cm; 34 GHz - 0,63 cm.
Mit γ=50° ist: β=32,9°, α=4,67°.

Materialien

Ausgabe des Arbeitsblatts für Schüler: Interferenzstreifen von Öl an der Wasseroberfläche, als html-Seite oder druckbare rtf-Datei
Ölverschmutzung und das Verhalten von Öl im Meer
Flugzeuggestützte Meeresüberwachung
Das Seitensichtradar
Das Mikrowellenradiometer
Ergänzung zu diesem Arbeitsblatt: Interferenzstreifen von Öl auf Wasser, als html-Seite: Lehrerausgabe, html-Seite: Schülerausgabe, oder druckbare rtf-Datei

Erforderliche Zeit

Zwei Schulstunden und/oder eine Hausaufgabe

Empfehlungen fü das Vorgehen an die Schülerinnen und Schüler

Erste Schulstunde:
- Bearbeiten Sie einzeln oder in Zweiergruppen die Fragen zu den physikalischen Eigenschaften von Öl und seinem Verhalten auf der Wasseroberfläche
- klären Sie, welche Hintergrundinformationen erforderlich sind, um diese Fragen zu behandeln
- Vergeben Sie an einzelne Mitglieder der Gruppe spezielle Aufgaben, die bis zur nächsten Stunde bearbeitet und gelöst werden sollen.
Dies sollte es Ihnen erlauben, die gestellten Fragen zu lösen und die Ergebnisse in der Klasse vorzustellen.

Bitte beachten: nicht jede weiter unten genannte Hintergrundinformation ist zur Bearbeitung der Fragen erforderlich. Entscheiden Sie selbst, welche Informationen wesentlich sind.
Hausaufgabe: Lösen Sie die von der Gruppe an Sie vergebene Aufgabe.
Zweite Schulstunde:
- stellen Sie Ihrer Gruppe vor, was Sie gelernt haben
- Diskutieren Sie, inwieweit Frage 4 mit Ihren Ergebnissen beantwortet werden kann
- stellen Sie Ihre Ergebnisse unter Nutzung der von Ihnen verwendeten Materialien vor.